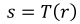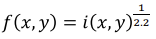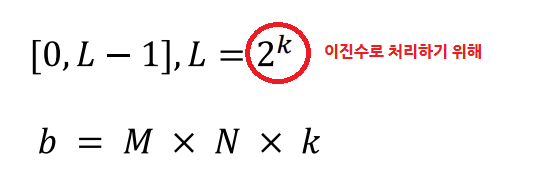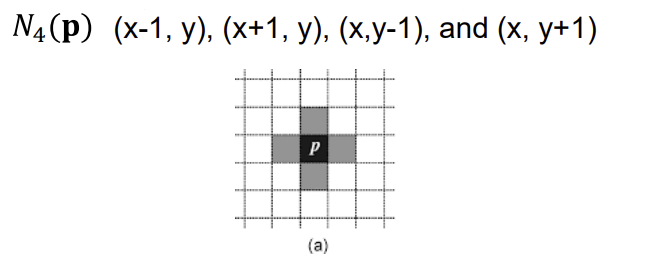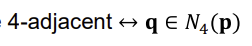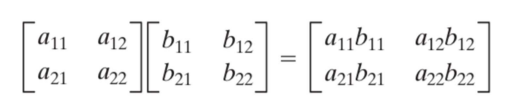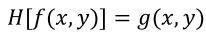VHAL_

** 해당 시리즈는 타블로그의 글을 참고하여 공부용으로 기록해놓은 글입니다 **

Basics

1. Intensity Trasnform (밝기값 변환)

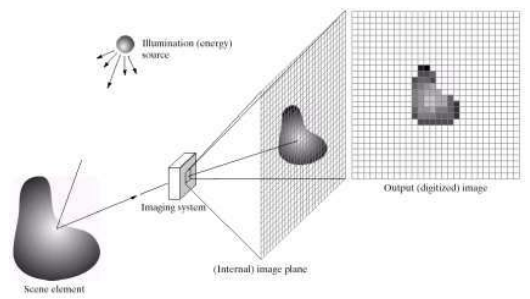
• 원본 이미지f의 밝기를 변환하여 출력 이미지g를 내보내는 함수T 

  

◾ Intensity Trasnform funtion T

(aka. grey-level function, mapping function)

• 기존 이미지의 픽셀값r을 s로 변환하는 함수T
  (T의 종류는 여러가지)

  

  

2. Spatial domain Operator (공간 영역 연산)

• 한 픽셀을 계산할 때 주변(neighbor, window)을 고려하는 것
• neighbor pixels의 평균으로 출력 이미지g를 얻음

  

  

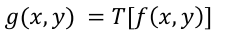
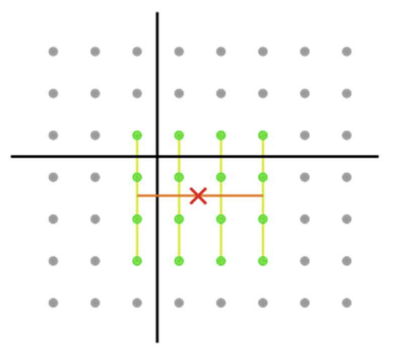
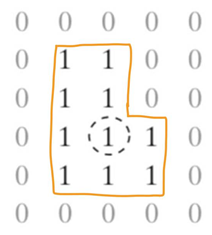
1. 4-neighbor Averaging

• 자신 포함 4이웃의 픽셀 값 평균으로 자신의 새로운 픽셀 값 얻음

  

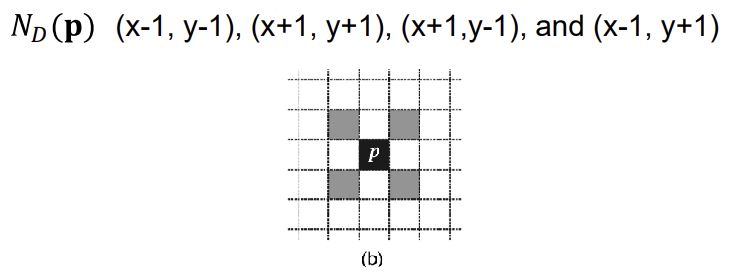
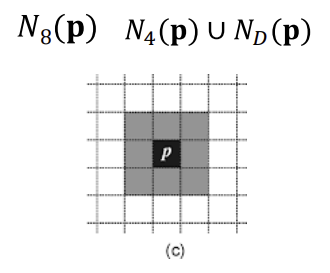
2. 8-neighbor Averaging

• 자신 포함 8이웃의 픽셀 값 평균으로 자신의 새로운 픽셀 값 얻음

  

3. Filtering

• Spatial domain operator를 filtering이라고 함
• 위의 Averaging을 한 값들의 집합

Intensity Transformation Functions 종류

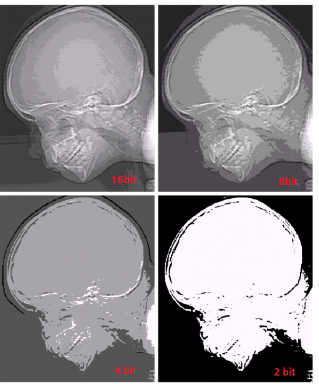
1. Image Negatives

• 원본 이미지의 범위 [0, L-1] 

  

  

2. Log Transformation

• 원본이미지가 0일 때 0이 나옴
• 상수 c

  

• 0은 0이고, 조금이라도 밝으면 밝게 나타남
• 어두운 부분의 디테일을 살리지만 밝은 부분의 디테일은 감소

  

3. Pow-Law (Gamma) Transformation

• Log Transformaion보다 자주 사용

  

  

• γ=1 -> 입력값 = 출력값
• γ<1 -> 어두운 부분의 디테일 살아남
• γ>1 -> 밝은 부분의 디테일 살아남
  
  
• 기울기가 클수록 디테일이 크게 살아남 (input이 작아도 대비(변화)가 높아진다)

• γ가 점점 감소하는 경우와 / 점점 증가하는 경우
  

  

❗감마가 낮아질 때 / 높아질 때의 기울기, 계수 등 그래프와의 관계 생각해보기

◾ Monitor response

• 모니터에서 가장 밝은 값은 대략 L = c^2.2
• 보통 실제 이미지들은 감마 연산을 거쳐서 저장된다.

  

• Linearization

  

4. Piecewise-Linear Transformation (부분선형변환함수)

• 좀 더 복잡한 변환 기능을 형성하기 위해 임의로 함수를 정의할 수 있음

  

• a - 기울기, 기울기가 가파를수록 대비가 높아져 어두움과 밝음의 구분이 쉬워짐 -> Contrast
• b - b가 양수면 전체 이미지가 밝아지고, 음수면 어두워짐 -> Brightness

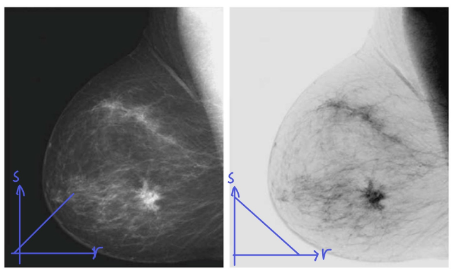
ex) Intensity Slicing

• 특정한 밝기 범위만 밝게하고 나머지는 억제

  

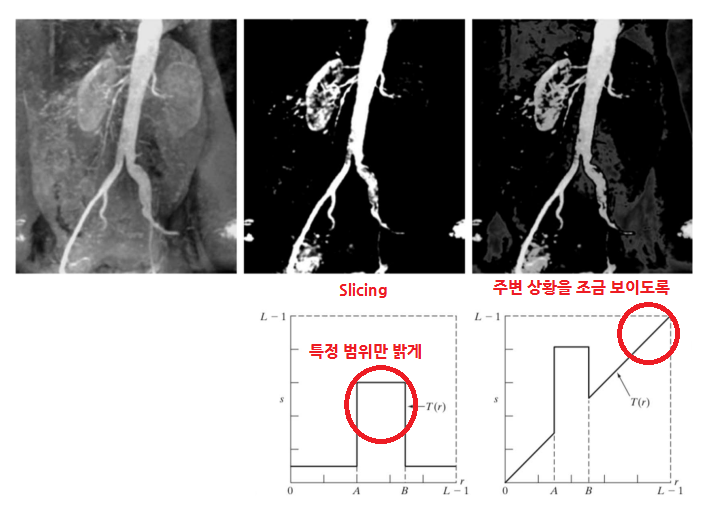
Histogram Processing

1. Image Intensity Histogram

• 각 밝기마다 해당하는 픽셀 수를 나타낸 그래프 (특정한 픽셀 값을이 존재할 확률) 

  

• 어두울 수록 왼쪽에 몰려있고, 밝으면 오른쪽에 몰려있다.

  

• 낮은 대비를 가지면 가운데 몰려있고, 대비가 높으면 고르게 잘 퍼져있다.

  

• 고르게 잘 퍼진 히스토그램을 만드는 것이 목표 (평탄화)

2. Probability distribution function (PDF, 확률분포)

• r의 밝기일 확률 = 특정 r의 밝기를 가진 픽셀의 수 / 전체

  

• 누적분포 = 0~r 까지의 확률의 합

  

• 평탄화(좋은 대비를 가지는 이미지)가 되려면 모든 히스토그램의 값이 상수면 좋겠다.

  

3. Histogram Equalization (히스토그램 평탄화)

• 평탄화되는 intensity transformation 함수
• x커지면 y도 커지는 단조함수(monotonically increasing)

  

  

  

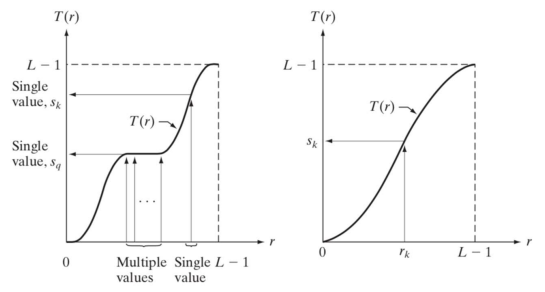
◾ Implementation

• r의 밝기일 확률의 누적분포와 s의 밝기일 확률의 누적분포가 같다

  

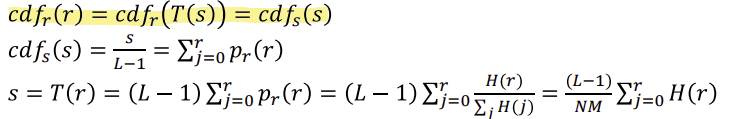
◾ Result

• 어둡든 밝든 거의 일정한 값(밝기)을 가진다 라는 특징을 가진다.
• 사람이 보기 좋다에 초점을 맞춘 것은 X

  

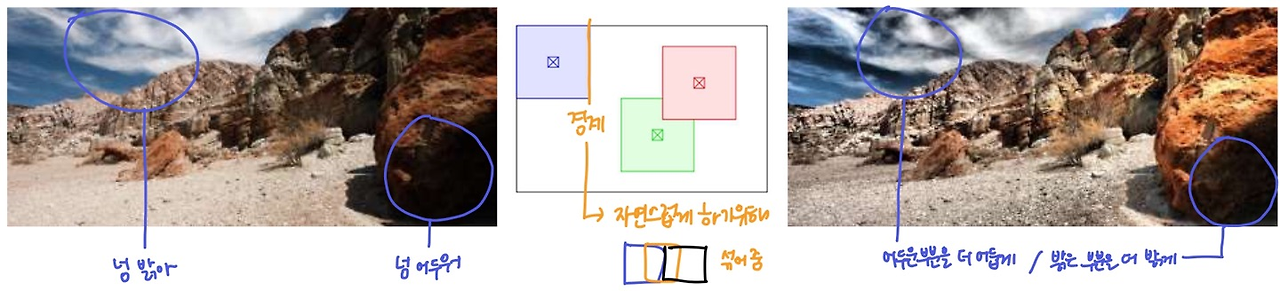
4. Local(adaptive) histogram equalization (AHE)

• global 정규화는 local 대비를 조절할 수 없기 때문에 window에서의 정규화를 해서 local의 대비를 조절한다.
• 구역마다 정규화 시 경계부분이 어색할 수 있기 때문에 옆 부분과 자연스럽게 섞어준다.

  

Spatial Filtering Fundamentals

1. Spatial Filtering (공간 필터링)

• 이미지를 공간적으로 필터링
• 미리 정의된 Operationw (kernel, mask, ...)
• Outputg는 고정, Inputf는 유동적

  

  

◾ Similar concept

1. Correlation(상관관계)

• 두 개의 독립적인 것들이 어떤 관계를 가지는가
• Spatial filtering과 같다.

1. Convolution

• 두 함수를 서로 곱해 합친다.

  

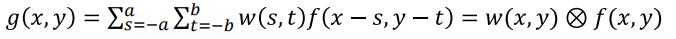
2. Padding

• 모서리 픽셀을 필터링하면 neighborhood가 존재하지 않는 부분도 생김.
• 그래서 네 모서리에 임의로 픽셀을 추가한다
  (실제로 이미지를 키우는 것은 아니고, 필요한 위치에서 픽셀을 참조해서 해당하는 값을 전달)

  

• Constant padding의 경우, 보통 0으로 채운다. (zero padding)

Smoothing Spatial Filters

• 위의 Spatial Filtering의 Operation w함수의 역할 중 하나
  
  
• 이미지를 부드럽게 만들기 위해 노이즈를 제거
• 해상도가 낮아짐

1. Averaging Filter (box filter)

• 노이즈 제거를 위해 주변에서 좀 튀는 픽셀을 주변과 비슷하게 바꿔줌
• neighborhood의 평균

  

  

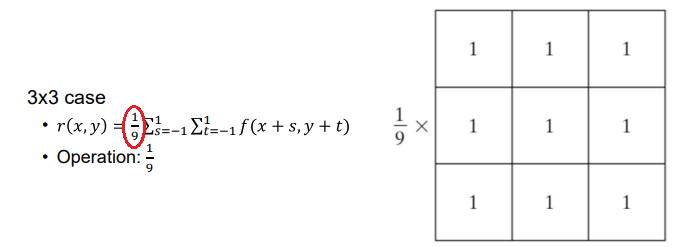
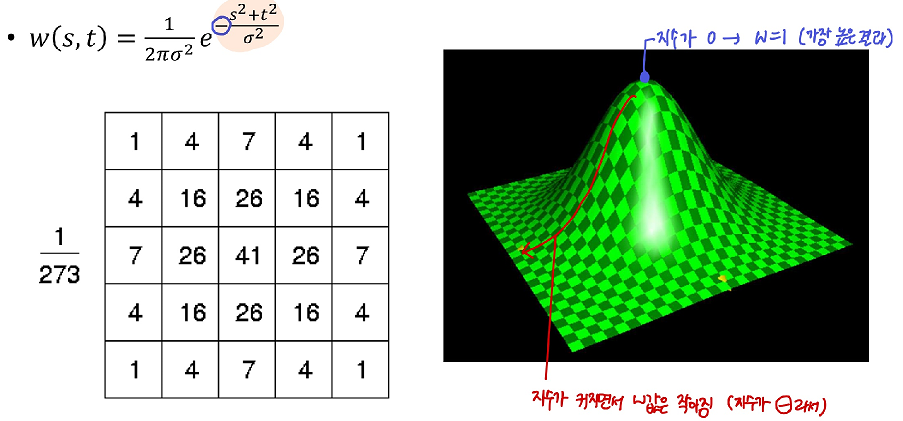
2. Weighted Averaging Filter (Gaussian)

• 위의 이미지처럼 averaging filtering을 많이 하면 보이는 경계를 보완하기 위한 방법
• 가까운 이웃의 비중을 살려서 평균을 구함

  

• 더 정교한 box(kernel)은 Gaussian

◾ Guassian

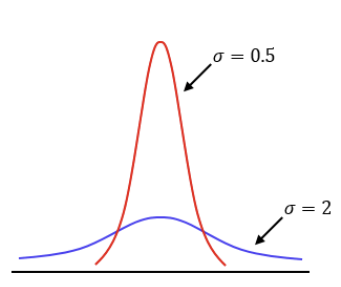
• 가우스 분포는 정규분포로 평균이 0, 표준편차가 σ이다.
• σ가 크면 납작하고, σ가 작으면 뾰족한 정규분포이다.

  

3. Separable Filter (linear)

• kernel이 큰 Operation은 시간이 오래걸린다. mxn
• 몇몇 Operator은 Separable한데, 이것은 가로 세로 커널로 분해 가능한 것을 의미한다.
• separable하면 시간은 m+n으로 줄어든다.
  
  
• 세로/가로 필터링을 따로 했을 때와, 전체 필터링 했을 때 결과가 같으면 Separable
• ex) box filter, Guassian filter는 Separable

  

4. Order-Statistic(median) Filters (Non-linear)

• 이웃 픽셀들을 정렬하여 찾은 중앙값으로 filtering
• 중심에서 멀리 벗어난 outlier를 삭제할 수 있다. (원본 이미지와 상관없이 noise가 큰 이미지) -> Gaussian과의 차이점

  

Sharpening Spatial Filters

1. Derivatives (미분)

• 이미지도 함수니까 미분이 가능하고, Finite difference라는 방식으로 이미지를 미분한다.

◾ Finite difference (Discretized version)

• 바로 옆 픽셀과의 차이f(x-1)-f(x)가 미분값
• 오른쪽, 왼쪽 둘 다 가능하다. 

  

• 미분을 한번 더 하는 경우는, 옆 픽셀과의 한번 미분한 값의 차이이다.

  

◾Edge (밝기가 변하는 부분)

• Ramp: 이미지 밝기가 서서히 변하는 edge
• Step: 이미지 밝기가 급격히 변하는 계단 형태의 edge

◾1번 미분

• 접선의 기울기 (이미지의 밝기 변화 정도)
• 0이면 일정한 밝기
• 0이 아니면 Edge
  (절댓값이 작은 부분은 Ramp, 큰 부분은 Step Edge)
• 극대점(미분값이 큰 부분)으로 Edge 검출

◾ 2번 미분

• 접선의 기울기의 증감 (이미지가 천천히 또는 빠르게 밝기 변화하는 정도)
• 0이면 일정한 정도로 밝기 변화
• 0이 아니면 갑자기 꺾어지는 Intensity trnasition 부분
• zero crossing가 발생하는 지점으로 명확한 Edge 검출

❗ 실제 영상에서는 Ramp Edge가 많기 때문에 1차로는 정확한 Edge 검출이 어려워서 2번 미분으로 명확한 Edge를 검출하는 것이다.

2. Laplacian

• 2차 미분의 zero crossing으로 엣지를 검출할 때 사용하는 연산
• 이미지 방향에 독립적이다. (Isotropic)

  

  

• 밝기의 불연속성을 강조하고, 느리게 변화하는 부분은 강조X
• 음수가 나올 수 있지만 0 이하는 전부 검정이다. 음수 부분을 확인하기 위해 Laplacian에 전체 상수를 더하면(곱하면?) 색 바뀌는 부분을 더 잘 확인할 수 있다.
  

  

3. Image Sharpening with Laplacian (샤프닝1)

• 상수c를 더한(곱한?) Laplacian 이미지를 원본에 더해 선명하게 만든다.

  

  

4. Unsharp Masking and Highboost Filtering (샤프닝2)

• box filter 또는 Gausian을 활용해 블러한 이미지f-를 원본 이미지f에서 빼서 세부 디테일 값Unsharp mask만 얻는다.
• 그 값을 원본에 더해 선명하게 만들어 최종 이미지g를 얻는다.

  

◾ 상수 k

• k=1 : Unsharp masking
• k>1 : Highboost filtering (더 선명하게)
• k<1 : Unsharp masking의 강조 감소 (선명해지긴 함)
• k<0 : blur와 비슷

5. Gradient

• 기울기, 증감, 변화도 와 같은 변화하는 정도를 나타냄
• 변화하는 정도가 가장 큰 부분은 일반적으로 edge와 모서리 부분이며, 이를 찾기 위해 gradient를 활용한다.
• 이미지(x, y)에서의 Gradient의 벡터값(방향, 크기)을 통해 해당 픽셀에서 edge까지 얼마나 가까운지, 방향이 어디인지 알 수 있다.

◾ 방향(gradient)

• f(x, y)에서의 최대 변화율의 방향 (이미지가 가장 밝아지는 방향)

  

◾ 크기(magnitude)

• 벡터 방향으로 얼마나 밝아지는지의 정도 (이미지가 밝아지는 픽셀까지의 거리)
• linear하지 않다.

  

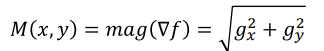
6. Gradient & Sobel Operator

◾ Basic gradient

• 중심 대칭이 아님

  

◾ Symmetric gradient

• 중심 대칭 (basic말고 이렇게 쓸 수도 있다~)

  

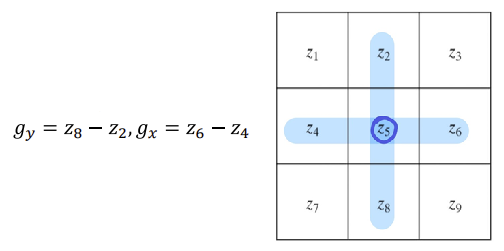
◾ Sobel Operator (3x3 version)

• noise의 영향을 줄이기 위해 주변 픽셀값도 섞어서 미분
• 중심이랑 가까운 부분z8,z2,z6,z4은 비중을 더 주기위해 더 많이 섞음
• 오른쪽 표에 있는 수의 합이 0이다.
• 왼쪽 식의 뜻 - 오른쪽 표에 있는 수를 각 픽셀에 곱하고 다 더한 값이 미분값이다.

  

  

• Laplacian은 2차 미분의 zero crossing으로 edge를 찾았고,
• Sobel(Gradient)은 x, y 방향의 1차 미분의 극대값으로 edge를 찾는다.
• 분류를 어케해야하는지 잘 머르겟다....................

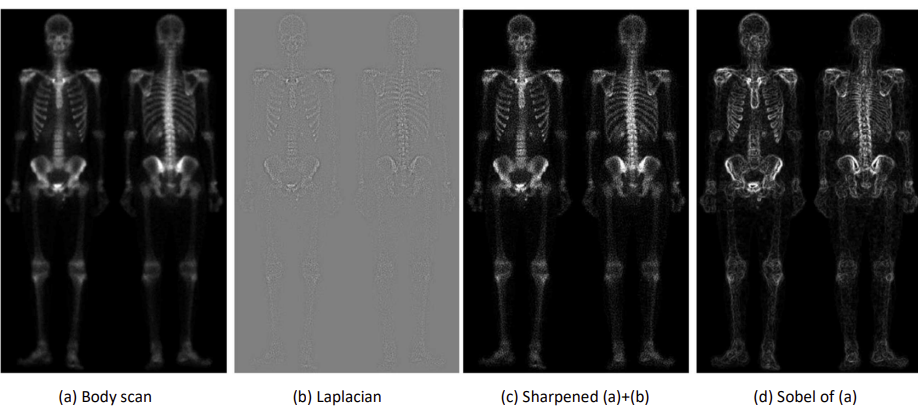
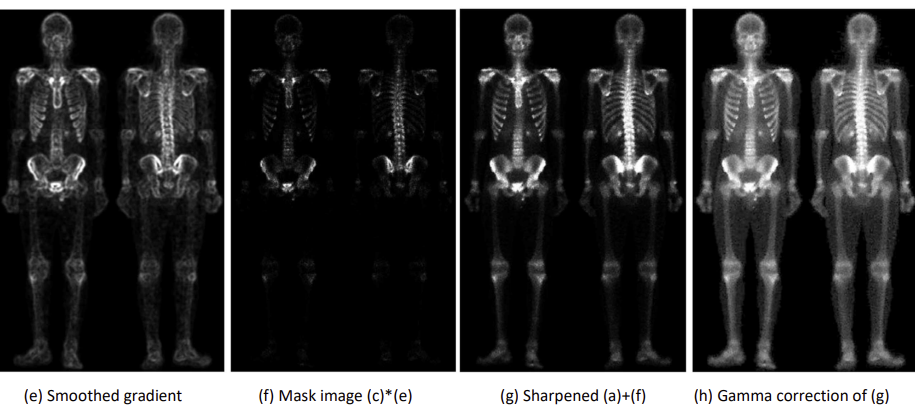
 Combining Spatial Enhancement

• 결국 지금까지 배운 공간 필터링을 조합해보면,, 이런 이미지를 만들어낼 수 있다. 잘 조합해서 쓰면 된다..?

  

  

** 해당 시리즈는 타블로그의 글을 참고하여 공부용으로 기록해놓은 글입니다 **

Human Vision

• Image Formation in the Eye 

  

 Lights

1. Human Vision

• Light Source (광원)
• 오브젝트로 향하는 광원 (Decay - 광원에서 멀어질수록 어두워짐)
• 오브젝트에 도착한 빛
  • Absorption (흡수)
  • Reflection(표면에서 반사) / Scarttering(내부로 흡수했다가 나옴)
• 오브젝트에서 눈으로 가는 빛 (No decay - 공기 저항 무시, 각 시세포가 받는 E는 일정)
• 눈에 도착한 빛 (Sensing Energy)

2. Light

• 특정 유형의 전자파인 Visible Spectrum(가시광선)만 사람 눈에 감지된다.

◾Color

• 다양한 wavelength(파장)의 light wave(광파) 혼합된 것이며 그 혼합물에 대한 사람의 반응, 느낌

◾ Achromatic light (무채색)

• 파장을 무시하는 빛으로 색은 없고 intensity(밝기)만 존재
  (aka. monochromatic, gray level, Luminace(휘도), birightness)
  
  

Image Acquisition

1. Sensor Element

• 빛 E가 들어오면 전류가 흐른다. (빛 신호 -> 전기 신호) 

  

  
  
  

1-1. Single Element Sensing

• sensor 하나가 좌우로 이동하고, 필름은 회전한다.
• 센서를 천천히 움직이면 해상도가 올라간다. (픽셀 개수가 정해지지 않음)
• ex) 잉크프린터, 필름 고해상도 현상 

  

1-2. Sensor Strip Sensing

• Sensor strip (여러개의 sensor)

  

• Sensor strip이 좌우로 이동한다.
• Sensor strip의 센서 개수가 해상도를 결정한다. (움직이는 방향의 해상도는 속도로 조절 가능)
• ex) 스캐너

  

1-3. Sensor Ring Sensing

• 동그란 모양의 Sensor Ring 사이로 3D오브젝트가 통과되며 이미지를 인식한다.
• 속도가 빠르다.
• ex) X-ray, CT

  

1-4. 2D Image Array Sensing

• 2D Sensor Array(센서가 이차원 배열로 존재)

  

• 렌즈(카메라) 필요
• 한 순간의 데이터를 저장할 수 있다. (snapshot)
• ex) CCD array

  

  
  
  

2. Image Formation Model

• 이미지가 디지털로 바뀌는 방법
• Image의 밝기: f(x, y)
  (밝기의 범위는 한계가 없다. 0 < f(x, y) < ∞)
• Formation model
  • Illumination (광원에서 나온 빛) : i(x, y)
  • Reflectance (반사율) : r(x, y)
  • 반사율 예시

    

• 광원에서 나온 빛과 반사율을 곱해 이미지의 밝기를 구한다.

  

  

3. Intensity Range (밝기의 범위)

• 한 픽셀의 값

  

• 이론에 따르면 밝기의 범위는 한계가 없어 0 < f(x, y) < ∞ 이지만, 센서가 받아낼 수 있는 최소, 최대가 정해져있다.

  

• 그래서 Intensity Range(Gray scale)는 보통 0에서 L-1까지의 값을 가진다.

  

  
  
  

Sampling and Quantization

1. Digitization

• 이미지를 디지털(정수 형태)로 바꾸는 과정

◾Sampling

• 연속적의 데이터를 다 알 수 없어서 이미지의 특정 공간만 Sampling해서 전체를 알기
• x, y방향으로 이미지를 작은 픽셀로 쪼개기
• 픽셀값으로 이미지를 나타냄 (각 픽셀마다 색, 밝기 등)

◾ Quantization (양자화)

• Sampling 값을 디지털화(정수화) 한다.
• 이미지의 경우 0-255 범위에 픽셀 정도가 저장된다. (사람이 구분할 수 있는 정도의 기준)
  

  

  

❗ Sampling과 Quantization 둘 다 무조건 많이 하는게 좋지만, 시간과 같은 자원의 한계가 있다.

2. Sampling

• 정수의 값을 갖는 몇개의 점xi yi에 대한 함수값

  

• 이차원 배열 / 행렬 형태

  

3. Quantization (양자화)

• [0~최대 밝기]의 범위를 정수로 쪼갬

  

• b와 k는 비례
• 수준이 높아질수록 자원이 많이 들고, 낮아지면 밝기 구분이 어려워짐

4. Saturation (색의 포화도)

• RGB가 전부 255를 넘은 Saturation 상태에서 다시 밝기를 낮추면 색이 복구되지 않고 회색이 나온다.

  

◾Clipping

• 모니터마다 가장 밝은 부분255의 밝기가 다 다르다.
• 카메라에서 밝기가 전체적으로 어두워지는 것은 기존의 255 밝기보다 낮은 밝기를 255로 Quantization하기 때문

5. Resolution (해상도)

1. spatial resolution (공간해상도)

• 이미지 구성에 사용되는 픽셀 수 (구별가능한 최소 단위)
• Dots per inch (DPI): 기준 크기에 단위(픽셀)가 몇개 들어가는지

  

2. Intensity resolution

• Intensity LevelL의 구별 가능한 최소 변화
• 각 픽셀이 가질 수 있는 값의 개수
• 8비트(가장 많이 사용), 12비트, 16비트 등
• Intensity level에 따른 이미지

  

◾Isopreference Curves

• ResolutionN이 높으면 Intensity Levelk이 낮아도 괜찮고, Resolution이 낮으면 Intensity Level이 높아지는 것이 좋다.
• 얼굴 이미지는 낮은 디테일, 군중 이미지는 높은 디테일을 가진다.

  

6. Image Interpolation

◾Interpolation

• 알고 있는 데이터로 모르는 부분을 추정한다. (ex-내적)

• 픽셀 사이의 값을 추정하여 더 높은 해상도를 만든다.

  

1. Nearest neighbor Interpolation

• 근처에 알고 있는 픽셀값으로 보간
• 경계선이 깨지며 해상도 낮아짐
  

  

  

2. Bilinear Interpolation

• 근처에 알고 있는 4개의 픽셀값을 적당히 섞은 새로운 값으로 보간

  

  

  

3. Bicubic Interpolation

• 근처의 16개의 픽셀값으로 3차 곡선을 만들어서 새로운 값으로 보간

  

  

✔️ 왼쪽부터 Nearest neighbor, Bilinear, Bicubic

🔵 Basic Relationship between Pixels

1. Neighborhood

• (x, y) 좌표를 가지는 픽셀p의 이웃

1. 4-neighborhood

2. 4 diagonal neighborhood

3. 8-neighborhood

2. Adjacency

• 픽셀 간 인접관계를 나타내기위한 Intensity valuse V

1. 4-adjacency

• 픽셀 q가 p의 4이웃이고, 두 픽셀 모두 V의 값을 가짐

  

2. 8-adjacency

• 픽셀 q가 p의 8이웃이고, 두 픽셀 모두 V의 값을 가짐

  

3. M-adjacency

• 두 픽셀 모두 V의 값을 가지는데,
  • 픽셀 q가 p의 4이웃 이거나
  • 픽셀 q가 p의 D이웃 이고 p의 4이웃과 qD이웃의 교집합에 V값을 가지는 픽셀이 없는 경우

    

3. Path (or Curve)

• adjacency한 애들 따라가서 다른 픽셀로 가는 길 (n - path의 길이)

  

• closed path - 시작해서 제자리로 돌아오는 path

  

• 두 픽셀사이 path가 있다 -> 두 픽셀이 connected
  

  

4. Region

• Path로 연결된 픽셀 덩어리 (connected set)

  

5. Boundary

• Region의 한 픽셀의 이웃 중, Region에 포함되지 않는 픽셀들
  (Region 픽셀 이웃의 여집합complement에 포함되는 픽셀)

  

6. Distance Measure (두 픽셀 사이 거리)

◾ Metric

• 거리를 재는 방법이 Metric하다는 것은
  1. 거리가 양수
  2. p -> q, q -> p 거리가 동일
  3. p -> q + q -> p ≥ p -> z
     

     

1. 직선거리

2. x축의 거리차 + y축의 거리차

• 4neighbor을 통해서만 측정하는 거리

  

3. x축 차이, y축 차이의 최대값

• 8neighbor을 통해서만 측정하는 거리

  

  
  

  

  
  
  

🟣 Mathematical Tools Basic

1. Array Operation

• 이미지끼리 곱할 때에는 아래 방법을 주로 사용 (기존의 행렬 곱셈이 아님)

  

2. Linear vs Nonlinear Operation

◾Operation

• f이미지를 넣어서 g이미지가 나오는 영상처리 함수H

  

1. Linear Operation

• H함수를 한 번에 적용한 것과 두 번에 나눠서 적용한 것의 결과값이 같으면 Linear
• 1번 적용한 것이 더 효율적

  

2. Nonlinear example

• Linear하지 않고 함수의 결과값이 다른 경우
  

  

3. Arithmetic Operation (산수 연산)

1. Addition

• 이미지를 픽셀별로 더하기
• [0, L-1]+[0, L-1]=[0, 2L-2] -> 범위가 달라진다.
• 보통 원본이미지f + Noiseη를 이미지라고 함

  

  

2. Subtraction

• 이미지를 픽셀별로 빼기
• [0, L-1]+[0, L-1]=[-L+1, L-1] -> 음수가 등장할 수 있음

  

  

3. Multiplication

• 이미지를 픽셀별로 곱하기 (행렬 곱하기 X)

  

  

4. Division

• 이미지를 픽셀별로 나누기

  

  

4. Logical Operation

5. Pixel-wise Logical Operation (픽셀 단위 논리연산)

1. Complement (여집합)

• 가장 큰 것K에서 뺀 것

  

2. Union (합집합)

• 두 이미지의 최대값을 취함
• ex) max(검정0, 회색160) -> 회색이 합집합

  

3. others

1. Image

• 특정 시간, 특정 방향의 빛의 Snapshot (시각적 자극을 비슷하게 나타냄)
• 사진이나 2차원 그림처럼 시각적 자극을 속이기 위해 만든 인공물
• Distributed amplitude of colors
  
  
• 2D function
  • 시각적 자극의 강도(intensity / amplitude)를 나타내는 함수f(x, y)
  • (x, y)는 2D 위치

2. Digital Image

• 이미지가 디지털 형태로 저장됨 (digital form / binary form)
• Digitization (이미지를 디지털로 바꾸는 방법)1. Raster(Bitmapped) Image
  • Finite set of digital values (Picture elements / pixels)
  • JPEG, PNG, GIF …
  2. Vector Image
  • 2D 평면에 어떻게 그림을 그릴 것인지에 대한 방법이 저장 (lines, polygons, circles, curves…)
  • Vecotor font, SVG, AI …
    
    
• 디지털 이미지의 장단점
  • 장점
    1. Easy reproduction (그리기 쉬움)
    2. Fine detail (정보 디테일 많음)
    3. Easy to access a part
    4. Easy to modify globally (전체 수정 쉬움)
  • 단점
    1. Large data
    2. Limited resolution (Bad for scaling)
    3. Hard to modify locally

3. Digital Image Processing

• 사람이 해석할 수 있도록 이미지 정보를 개선
• 저장, 전송, 자율 시스템 인식을 위한 표현
  
  
• Fundamental Levels (Low level - 영처 / Mid, High level - 컴비) 

  

  
  
  
• Key Stages in DIP

1. Image Acputstion (이미지 입력) 

   

2. Image Enhancement (이미지 향상) - 저화질을 고화질로

   

3. Image Restoration (이미지 복원)

   

4. Morphological Precessing

   

5. Segmentation (영상 분할) - 이미지 내에 있는 객체들을 의미있는 단위로 분할

   

6. Object Recognition (객체 인식)

   

7. Representation & Description